自由空間中的靜電
靜電學是電磁學的一個子領域,研究靜(非運動)電荷引起的電場。我們首先從自由空間開始討論,假設空間電荷密度為 ,它與電場
的關系式如下:
(1)

其中, 是自然界的一個普適常數,稱為自由空間的介電常數。
這一關系意味著,在靜電學中,空間電荷密度相當于一個體積源。只有電荷-電場關系是不夠的,但麥克斯韋方程組隱含了一個額外要求,即電場為無旋場(無旋度):
(2)

這是用于描述靜電場的法拉第定律。

兩塊電容板周圍的靜電場 便是無旋矢量場的一個例子。
無旋場存在一個標量勢,由此可以得到電勢 的定義:
(3)

對于任何足夠平滑的標量場 來說,總會滿足以下矢量恒等式,確保電場為無旋場:
(4)

電勢前面的負號是傳統約定。

兩塊電容板周圍的電勢場 。
通過組合以上表達式,只用一個方程即可描述麥克斯韋靜電方程中包含的信息:
(5)

由于此方程不能表示電介質材料,因此在工程領域的應用有限。為了解決這個問題,我們利用感應極化效應對該理論進行擴展。
電介質材料中的靜電
理想化電介質材料的特點在于其中沒有任何自由電荷,而只有束縛電荷。在微觀層面,這些束縛電荷可以被外部電場所取代,從而產生感應電偶極子。這些感應電偶極子是成對的正負電荷,在某種程度上與電場方向一致,導致電介質材料內的電場與自由空間的電場不同。為了從宏觀上描述這種現象,我們可以方便地引入極化矢量場 和極化電荷密度
,其關系式為:

根據下式,極化效應會局部改變材料內部的電場:

在此基礎上,我們可以引入一個新的基本量,即電位移場 ,定義為:

利用這一定義,靜電方程(也稱為高斯定律)可以變為:
(10)

為了充分描述靜電現象,我們仍需保留電場無旋(法拉第定律)條件。由于此條件用電勢來描述,因此靜電方程組可以聯立成一個方程:
(11)


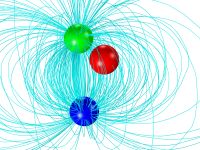
介電常數大于周圍環境的物體附近的電場。這兩幅圖顯示位于兩塊電容板(未顯示)之間,被空氣( )包圍的電介質體(
)。頂部和底部電極分別具有正電位和負電位。左圖用不同的顏色來顯示電場
大小,并用箭頭表示其方向。右圖用不同的顏色來顯示電位移場
幅值,也用箭頭表示方向。紅色和藍色分別表示高低幅值。
線性電介質材料
在靜電學中,人們常常可以假設材料呈線性,這預示著極化矢量場與電場成正比:
(12)

其中比例常數 為電極化率。
當材料呈各向異性時,極化率可以是一個 3x3 的張量:
(13)

將其代入 與
的關系式中,得到:
(14)

我們還可以引入兩個有用的新量:相對介電常數 和絕對介電常數
。
線性電介質材料最重要的本構關系假定為:
(15)
各向異性極化率對應于各向異性相對介電常數:
(16)

這意味著對于某些材料而言, 和
場可能不完全一致。
利用靜電勢,我們可以將線性材料中的靜電基本方程寫為:
(17)
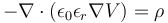
材料界面的靜電方程和邊界條件
高斯定律和法拉第定律可以分別看作是為電場散度和旋度指定條件。根據亥姆霍茲定理,這可以確定電場所能達到的場強常數。順便指出一點,由于這個未知常數,我們最終必須指定電勢的地電平。在材料界面處,散度條件表示電場法向分量的條件,旋度條件表示電場切向分量的條件。材料界面表明存在不連續,為了方便理解要對邊界施加何種條件,我們通常使用對應的積分形式。然后,通過分別采用閉合面的收縮極限(高斯定律)和封閉等值線的收縮極限(法拉第定律),使材料的界面形成封閉,導出邊界公式。
下表對此進行了匯總:

其中, 是體積電荷,
是材料界面處的表面電荷。

通過文字表述來匯總這些方程的含義可以幫助你加深理解:
| 方程名稱 | 微分形式 | 積分形式 | 邊界條件 |
|---|---|---|---|
| 高斯定律 | 所有電場線都始于電荷,并終止于電荷。 | 通過閉合面的總通量等于其所包圍的電荷。 | 材料界面的表面電荷等于位移場法向分量的躍遷。 |
| 法拉第定律(靜電) | 電場為無旋場。 | 電場守恒。 | 在整個材料界面上,電場的切向分量是連續的。 |
需要注意的是,對于時變情況,電場不再是無旋場,并且法拉第定律會得到一個與電磁感應對應的附加項。
靜電能
電場中包含的靜電能可以用許多不同的方式來表示。對于電介質,某一體積( )內的靜電能可以用場量表示為:

其中,靜電能量密度定義為:

請注意,對于靜電能量密度的定位,相關的物理說明比較有限(另請參見:The Feynman Lectures on Physics, Volume 2)。
另一個用體積電荷密度 和局部電勢
來描述靜電能的表達式為:

這兩個能量表達式被證明是等價的。
在計算靜電力和電容值時,靜電能的概念非常有用。
經授權轉載自 COMSOL 多物理場仿真百科,原文鏈接:
靜電學理論簡介“多物理場仿真百科”旨在幫助大家了解各種相互作用的物理場背后的基本概念和理論,并提供多物理場耦合仿真的相關知識。
多物理場仿真百科理解什么是多物理場以及多物理場耦合方法,從傳遞現象、電磁場理論和固體力學等第一性原理出發,將其作為實現軟件功能的基本構成要素,根據具體的仿真需求,用戶可以條理清晰地將這些基本要素組合在一起來解決自己的問題。
 鍋爐之家客服熱線:
鍋爐之家客服熱線:














