你有沒有遇到過這樣一種情況：在笛卡爾平面內(nèi)，有一組非均勻分布的點(diǎn)，用于對(duì)面高度進(jìn)行采樣，例如地圖等高線上的點(diǎn)或表示某些材料屬性數(shù)據(jù)的數(shù)據(jù)點(diǎn)？你可能還想過，要在這些點(diǎn)之間重建或插值出一個(gè)連續(xù)的光滑曲面。對(duì)于這種想法，你可以使用 COMSOL Multiphysics 的核心功能，即徑向基函數(shù)來構(gòu)建這樣的曲面。讓我們來看看應(yīng)該如何操作。

徑向基函數(shù)簡介

class="nolink">徑向基函數(shù) (RBF) 通常是指根據(jù)到某點(diǎn)的距離（或半徑）定義的任意函數(shù)：

(1)

式中，w 是徑向基函數(shù)的權(quán)重； 是該點(diǎn)的坐標(biāo)或中心；r 是從 XY 平面內(nèi)的任意其他點(diǎn)到此中心的距離。

徑向基函數(shù)本身可以是許多不同類型函數(shù)的一種。多諧波樣條系列通常用于插值，特別是薄板樣條函數(shù)，這種基函數(shù)的形式為：

(2)

僅僅這樣一個(gè)徑向基函數(shù)并不是那么吸引人，但我們可以在有限數(shù)量的具有不同權(quán)重的不同中心上進(jìn)行求和，并選擇性地添加具有權(quán)重的線性多項(xiàng)式項(xiàng) 從而得到函數(shù)：

(3)

如果有足夠的中心點(diǎn)，那么一組基函數(shù)的總和可以用來表示非常復(fù)雜的單值函數(shù)。當(dāng)使用薄板樣條基函數(shù)時(shí)，還有一個(gè)額外的優(yōu)點(diǎn)，就是這個(gè)函數(shù)在任何地方都是平滑的，并且可以無限微分。

現(xiàn)在讓我們來看看如何使用這些徑向基函數(shù)來插值得到光滑曲面。如果我們獲得一組有限的中心點(diǎn)位置 ，以及它們對(duì)應(yīng)的已知高度 ，那么可以寫一個(gè)線性方程組：

(4)

其中，系統(tǒng)矩陣項(xiàng) 是各中心點(diǎn)之間計(jì)算的徑向基函數(shù)。

當(dāng)使用薄板樣條基函數(shù)時(shí)，幾乎所有的非對(duì)角線項(xiàng)都是非零的，因此這個(gè)系統(tǒng)矩陣非常密集。線性系統(tǒng)可以求解所有權(quán)重，我們可以計(jì)算 xy 平面中任何其他點(diǎn)的加權(quán)徑向基函數(shù)之和，從而得到平滑插值函數(shù)。現(xiàn)在，讓我們看看如何使用 COMSOL Multiphysics 的核心功能來計(jì)算這些權(quán)重并將插值函數(shù)可視化。

使用 COMSOL Multiphysics 中的徑向基函數(shù)進(jìn)行曲面插值

我們從建立一個(gè)包含三維組件的模型開始，該模型使用無量綱單位系統(tǒng)，可以在組件 1 的設(shè)置中選擇單位系統(tǒng)。如果我們的數(shù)據(jù)代表材料屬性而不是幾何形狀，則無量綱單位系統(tǒng)使用起來更簡單。

模型中的幾何圖形由兩個(gè)特征組成。首先，點(diǎn) 特征用于定義點(diǎn)集（可以從文本文件復(fù)制坐標(biāo)列表）。累積選擇 用于定義所有這些點(diǎn)的命名選擇，如下面的屏幕截圖所示。此外，還有一個(gè)長方體 特征，其尺寸略大于數(shù)據(jù)點(diǎn)的范圍，并被定位為包住所有數(shù)據(jù)點(diǎn)。

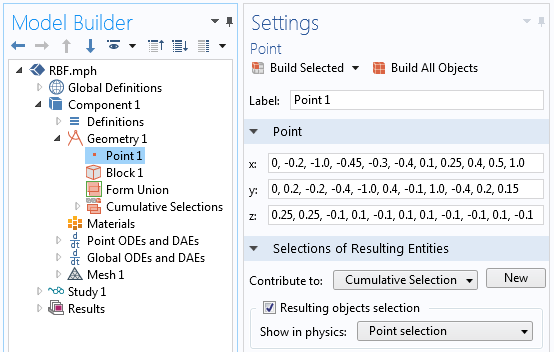
定義幾何圖形后，我們在剛剛創(chuàng)建的點(diǎn)上定義一個(gè)積分組件耦合 算子。由于積分是在一組點(diǎn)上完成的，因此這個(gè)運(yùn)算符等效于獲取在一組點(diǎn)上計(jì)算的表達(dá)式總和。接下來，我們定義三個(gè)變量，如下面的屏幕截圖所示。

首先，變量 r = eps+sqrt((dest(x)-x)^2+(dest(y)-y)^2) 將用于計(jì)算所有中心之間的距離。請(qǐng)注意運(yùn)算符 dest() 的用法，這會(huì)強(qiáng)制在目標(biāo)點(diǎn)而不是源點(diǎn)上計(jì)算運(yùn)算符中的表達(dá)式。添加一個(gè)非常小的非零項(xiàng)（eps 是機(jī)器精度），以使這個(gè)表達(dá)式永遠(yuǎn)不會(huì)為零。

接下來，變量 phi = r^2*log(r) 是方程(2)中的薄板樣條基函數(shù)。請(qǐng)注意，當(dāng)半徑為零時(shí)，此函數(shù)應(yīng)該收斂為零，但由于對(duì)數(shù)函數(shù)的原因，我們確實(shí)需要使半徑不能完全為零，以便可以在零處也能計(jì)算基函數(shù)。還值得一提的是，這個(gè)函數(shù)可以更改為任何其他所需的基函數(shù)。

最后，定義 RBF = intop1(w*phi)+a0+a1*x+a2*y 是方程(3)，即插值曲面本身，其權(quán)重尚未計(jì)算。請(qǐng)記住，積分組件耦合算子用于獲取算子中的表達(dá)式在這些點(diǎn)上的總和。

現(xiàn)在幾何已經(jīng)設(shè)置好了，所有變量都已定義，我們已經(jīng)準(zhǔn)備好求解徑向基函數(shù)和多項(xiàng)式項(xiàng)的權(quán)重了。這是通過點(diǎn)常微分 和微分代數(shù)方程 接口在我們要插值的點(diǎn)上進(jìn)行定義而完成的，如下面的屏幕截圖所示。我們可以將所有單位設(shè)置為無量綱，因?yàn)辄c(diǎn)位置也是無量綱的。這些設(shè)置定義了一組未知數(shù) w，每個(gè)點(diǎn)將具有不同的值。

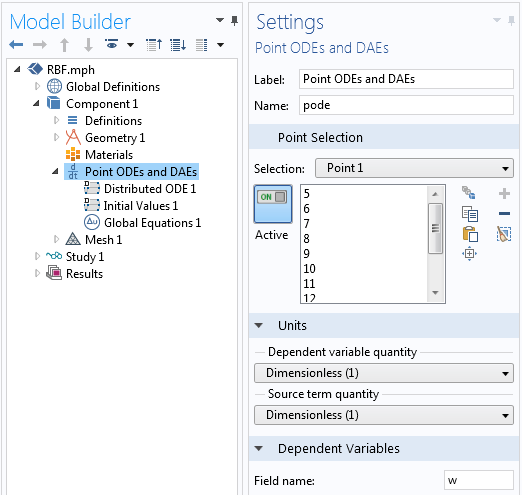
在這個(gè)物理場接口中，只需要修改兩個(gè)特征。首先，需要調(diào)整分布式常微分方程 的設(shè)置，如下圖所示。源項(xiàng) 定義為 z-RBF。由于求解穩(wěn)態(tài)研究時(shí)方程中的所有其他項(xiàng)均為零，因此該項(xiàng)表示在所有選定點(diǎn)處 RBF=z。使用這個(gè)功能，我們可以定義等式(4) 的第 1 行到第 N 行。

其次，我們需要定義等式(4)的最后三行。這是通過全局方程 功能完成的，如下面的屏幕截圖所示，這三個(gè)方程求解權(quán)重 a0，a1 和 a2。同樣，積分耦合運(yùn)算符用于獲取所有選定點(diǎn)的表達(dá)式之和。有了這兩個(gè)特征，問題的定義就完整了，差不多可以進(jìn)行求解了。

求解這個(gè)模型要求我們在所有點(diǎn)上都有一個(gè)網(wǎng)格，因此我們在邊界框上應(yīng)用了自由四面體網(wǎng)格，然后使用穩(wěn)態(tài)求解器求解。完成求解后，我們就可以繪制變量 RBF 的插值函數(shù)，如下所示。

將功能打包到一個(gè)仿真 App 中

如果你想直接使用這個(gè)功能，而不用在自己的模型中設(shè)置所有這些功能，歡迎你從 COMSOL 案例庫中下載我們的演示仿真 App，其中可以從一個(gè)用逗號(hào)分隔的文件中獲取 xyz 數(shù)據(jù)點(diǎn)并計(jì)算插值曲面。使用此演示 App 最多可以插值 5000 個(gè)數(shù)據(jù)點(diǎn)。

除了對(duì)曲面進(jìn)行計(jì)算之外，這個(gè) App 還可以導(dǎo)出描述曲面的完整分析函數(shù)，以及它的 COMSOL 格式的 CAD 文件，所有這些都是 COMSOL Multiphysics 的核心功能。CAD 數(shù)據(jù)是 NURBS 表面，因此僅近似表示函數(shù)，但對(duì)于相當(dāng)光滑的曲面，精度非常高。該仿真 App 用戶界面的屏幕截圖如下所示。

自己動(dòng)手嘗試

點(diǎn)擊下方按鈕，下載仿真 App，嘗試使用仿真 App 計(jì)算一組點(diǎn)之間的插值：

更多資源

如果你有興趣了解有關(guān)模型開發(fā)器 和 COMSOL Server? 的更多信息(它們可用于開發(fā)和運(yùn)行此仿真 App)，請(qǐng)查看以下資源。

• 閱讀 App 開發(fā)器簡介手冊中的完整說明摘要
• 觀看視頻，了解如何使用 App 開發(fā)器和 COMSOL Server?
• 閱讀博客文章，了解如何在各種應(yīng)用中使用仿真 App

你想使用 COMSOL Multiphysics 做什么？你對(duì)徑向基函數(shù)的功能還有其他疑問嗎？歡迎聯(lián)系我們尋求幫助。