Newman 模型及其衍生模型構(gòu)成了一套標(biāo)準(zhǔn)理論，該理論能夠準(zhǔn)確地預(yù)測鋰離子電池在一系列工作條件下的設(shè)計性能。當(dāng)使用 Newman 模型時，人們不必細(xì)致地描述電池電極的多孔結(jié)構(gòu)，而只需要將常見的平均尺寸用作輸入，即可將電極表征為均相的各向同性材料。然而，與詳細(xì)的非均相幾何模型相比，這種方法的準(zhǔn)確度如何呢？讓我們來一探究竟吧。

鋰離子電池的不同建模方法

在鋰離子電池建模領(lǐng)域，Newman 模型及其衍生模型占據(jù)著主導(dǎo)地位。由于此類模型基于多孔結(jié)構(gòu)的均相化，所以使用者無需再詳細(xì)描述多孔電極的三維幾何結(jié)構(gòu)。

均相 Newman 模型

在模型中，均相化是指通過將真實的多孔結(jié)構(gòu)被處理成固體粒子（上方左圖中的藍(lán)色部分）和孔隙電解質(zhì)（綠色部分）組成的均勻混合溶液，從而將多孔結(jié)構(gòu)近似表示為一個塊厚板。采用均相化表征帶來的結(jié)果之一是：孔隙電解質(zhì)（離子導(dǎo)體）和電極中的導(dǎo)電顆粒（電子導(dǎo)體）被定義在了同一個幾何域中。之后，我們使用孔隙率和迂曲度等變量來對有效電荷和質(zhì)量傳遞屬性進行描述，進而考察孔隙結(jié)構(gòu)和顆粒對幾何形狀的顯著影響。

均相多孔電極模型包含了在電極材料和孔隙內(nèi)電解質(zhì)之間電荷轉(zhuǎn)移反應(yīng)，此反應(yīng)在實現(xiàn)電流傳輸?shù)耐瑫r，也充當(dāng)了電極和電解質(zhì)區(qū)域電流的源和匯，并實現(xiàn)二者平衡，該反應(yīng)類似溶液中兩種化學(xué)物質(zhì)之間均相反應(yīng)。陰極的電荷轉(zhuǎn)移反應(yīng)是導(dǎo)體的平衡電流的源，同時也是用于維持孔隙電解質(zhì)電流平衡的匯。采用上述的源和匯，根據(jù)法拉第定律和均相電荷轉(zhuǎn)移反應(yīng)的化學(xué)計量系數(shù)，可以實現(xiàn)模型中材料平衡的計算。

這些多孔電極模型對各類電化學(xué)電池中的多孔電極的建模和仿真幫助很大。但在描述鋰離子電池多孔結(jié)構(gòu)的詳細(xì)設(shè)計時，這些模型是否有效呢？結(jié)論是：只有將均相模型與非均相模型進行比較，才能知道這個問題的答案。為此，我們創(chuàng)建了一個非均相模型，以驗證 Newman 模型對理想的三維多孔電極仿真的有效性。

創(chuàng)建非均相模型

在非均相模型中，我們明確地將導(dǎo)電顆粒和孔隙間電解質(zhì)描述為三維結(jié)構(gòu)，并在空間建模時將二者處理成兩個獨立的域。

離子遷移導(dǎo)致的電流守恒僅限于孔隙內(nèi)電解質(zhì)域，而導(dǎo)電顆粒的電流守恒僅限于固體電極區(qū)域。離子的質(zhì)量傳遞僅定義在孔隙電解質(zhì)域內(nèi)，與此同時固體顆粒的表面存在一個邊界，在該邊界上，離子或溶液中的其它物質(zhì)可以通過相間的電子轉(zhuǎn)移進行反應(yīng)。上述模型與均相模型形成了鮮明的對比，因為在均相模型中，材料平衡和反應(yīng)均定義在整個均相電極的計算域中。

在模擬固體粒子表面形成的金屬鋰時，假設(shè)其僅在顆粒域中擴散，其中顆粒表面充當(dāng)了外部邊界。

評估 Newman 模型的準(zhǔn)確性

現(xiàn)在，我們可以開始對比Newman 模型和非均相模型哪一個可以更加有效地用于描述精細(xì)的三維模型。建模實驗十分簡單：我們構(gòu)建了一個包含理想三維多孔結(jié)構(gòu)的理想電池單元，左右兩側(cè)的多孔結(jié)構(gòu)相當(dāng)于鋰離子電池中的負(fù)極和正極。最終的幾何模型如下圖，其中流線的作用是說明自由電解質(zhì)和孔隙內(nèi)電解質(zhì)中的電流流向。電極粒子由長軸方向各異的橢球組成，形成了導(dǎo)電陣列，電解質(zhì)包含在粒子之間的空隙中。

上圖顯示了放電過程中固體粒子表面的電荷傳遞導(dǎo)致的電流密度的絕對值。在圖中，正負(fù)電極面向集流體一側(cè)比面向自由電解質(zhì)（或分離膜）一側(cè)的使用率更低。

我們可以通過旋轉(zhuǎn)粒子的長軸方向，從而得到兩種不同的沿電極長度方向的孔隙率分布，同時保持空隙-固體比率（孔隙率）總體不變。因為 Newman 模型只使用總體的的平均孔隙率作為輸入條件，當(dāng)電極結(jié)構(gòu)發(fā)生上述變化，其計算結(jié)果沒有變化。

若將圖3 中的電極旋轉(zhuǎn) 180°，比如旋轉(zhuǎn)下圖中箭頭所處的正電極，電流密度分布將隨之變化，但是這種變化非常小（兩張圖的顏色圖例對比說明了這一點）。即使使用電化學(xué)阻抗譜也很難檢測出該電流分布的細(xì)微差異，對此我們將在下文進行探討。

可以使用類似于電化學(xué)阻抗譜（electrochemical impedance spectroscopy，簡稱 EIS）的方法，將不同時間尺度的電極的子過程進行分離，也許有能力捕捉到不同幾何結(jié)構(gòu)導(dǎo)致電流分布產(chǎn)生的差異。為此，我們分別采用非均相幾何模型和均相 Newman 模型對 EIS 實驗進行模擬。

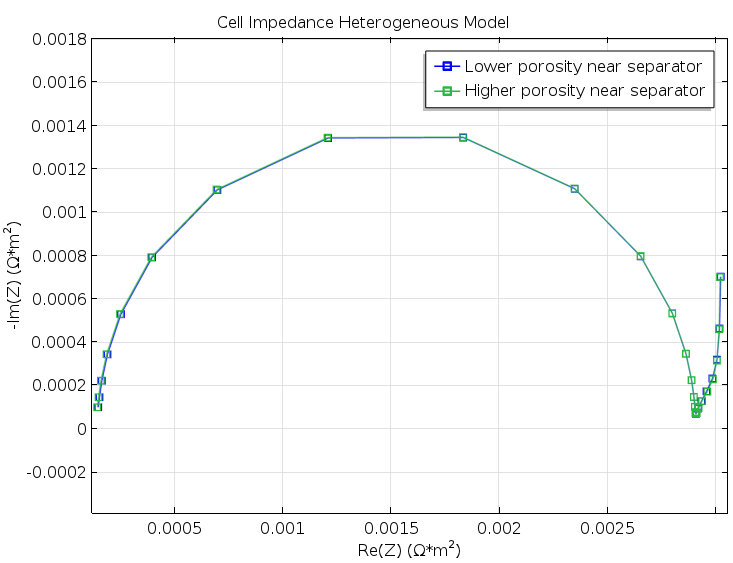
實驗結(jié)果喜憂參半。令人失望的是，如圖 5 所示，通過對兩個幾何結(jié)構(gòu)進行模擬，我們得到的奈奎斯特圖并沒有顯示圖 3 和圖 4 中的細(xì)微變化；令人驚喜的是，在沒有任何參數(shù)擬合的情況下，Newman 模型與非均相模型表現(xiàn)出良好的一致性，具體請參照下圖。這實在有點令人驚訝，因為我們的理想化結(jié)構(gòu)在細(xì)節(jié)之處似乎過于粗糙，無法有效地進行均相化。舉例來說，粒子尺寸比所模擬電池單元的寬度僅僅小一個數(shù)量級。

關(guān)于使用 Newman 模型和非均相模型模擬鋰離子電池的總結(jié)

當(dāng)然，最后還有一點！我們在上文中創(chuàng)建了一個簡單的幾何結(jié)構(gòu)，并通過旋轉(zhuǎn)電極使其結(jié)構(gòu)發(fā)生變化，也許該變化太細(xì)微以至于無法給結(jié)果帶來顯著的影響。下一步自然是保持平均屬性固定不變，嘗試對詳細(xì)幾何模型進行更大幅度的更改。這樣一來，我們就有可能捕捉到不同的非均相結(jié)構(gòu)導(dǎo)致的結(jié)果差異，而這是均相的 Newman 模型無法實現(xiàn)的。

想自己動手嘗試建模嗎？請至 COMSOL 官網(wǎng)查看文中設(shè)計的模型，同時還能下載用于生成仿真結(jié)果的 COMSOL Multiphysics 文件。您可以對模型進行任意的更改，并以此基礎(chǔ)建自己的幾何模型。