本文我們將繼續(xù)對(duì)線性系統(tǒng)諧波激勵(lì)建模進(jìn)行討論，現(xiàn)在把重點(diǎn)轉(zhuǎn)移到非線性系統(tǒng)。我們將研究系統(tǒng)的載荷上有一些正弦分量的問題，以及材料屬性或載荷和約束直接取決于解的情況。在這篇文章中，你將看到 COMSOL Multiphysics 能用一些非常有效的求解算法解決這些明顯的非線性問題。讓我們來了解一下。

帶有時(shí)間諧波分量的載荷和非線性系統(tǒng)

在之前一篇關(guān)于線性系統(tǒng)諧波激勵(lì)建模的文章中，我們確定了兩個(gè)條件，在這兩個(gè)條件下，可以在頻域中對(duì)系統(tǒng)的瞬態(tài)響應(yīng)進(jìn)行建模。這兩個(gè)條件是：

1. 系統(tǒng)上的所有隨時(shí)間變化的載荷和約束必須以相同的固定頻率正弦變化。
2. 所有的載荷、約束和材料屬性必須與解無關(guān)。

今天，我們將研究如何將這兩個(gè)假設(shè)放寬一些。我們從一個(gè)非常常見的系統(tǒng)案例開始討論：一個(gè)拉緊的吉他弦的振動(dòng)。在這個(gè)示例中，載荷在時(shí)間上并不是純正弦的變化。我們都知道，當(dāng)增加吉他弦的張力時(shí)，音高(振動(dòng)的基本頻率)會(huì)增加。

讓我們先使用之前文章中的通用偏微分方程來考慮這種情況。(1)

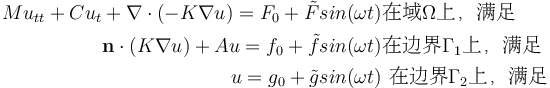
其中，體載荷 、邊界載荷 和約束條件 ，被分解為一個(gè)常數(shù)分量和一個(gè)正弦時(shí)變分量。對(duì)于一個(gè)結(jié)構(gòu)工程師，你可以將其稱為靜態(tài)和動(dòng)態(tài)分量的分解。對(duì)于一個(gè)電氣工程師，你會(huì)把這些單元分別描述為直流和交流分量。

我們可以進(jìn)一步假設(shè)動(dòng)態(tài)分量的大小比靜態(tài)分量小得多，也就是 ， 和 。如果動(dòng)態(tài)載荷相對(duì)較小，那么可以合理地假設(shè)動(dòng)態(tài)載荷將導(dǎo)致靜態(tài)載荷情況下的小振蕩。也就是說，我們假設(shè)解將采取以下形式： 。這也稱為諧波擾動(dòng)，或頻域擾動(dòng)。在 COMSOL Multiphysics 中，我們把這稱為結(jié)構(gòu)力學(xué)物理場(chǎng)接口的預(yù)應(yīng)力分析 研究；電磁學(xué)物理場(chǎng)接口的小信號(hào)分析 研究；以及電化學(xué)物理場(chǎng)接口的交流阻抗 研究。

這些研究類型都有相同的底層解決方法。他們一開始就忽略了隨時(shí)間變化的正弦波分量，首先解決穩(wěn)態(tài)問題。

(2)

實(shí)際上，材料屬性和載荷都可以直接依賴于解。即 。這意味著，穩(wěn)態(tài)問題實(shí)際上可以是非線性的，只要材料的非線性、靜載荷和約束條件的組合是一個(gè)良好的問題，這并不會(huì)使分析變得真正復(fù)雜。如果想要更好地了解如何解決這種非線性穩(wěn)態(tài)問題，請(qǐng)閱讀我們的求解器系列文章。

(3)

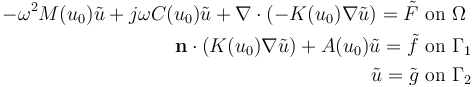
對(duì)于結(jié)構(gòu)問題，穩(wěn)態(tài)解也將代表系統(tǒng)的已變形狀態(tài)。頻域擾動(dòng)方程是在這個(gè)變形狀態(tài)上形成的，除了材料非線性之外，還引入了所謂的幾何非線性。上述控制方程也可以通過對(duì)所有載荷和約束條件進(jìn)行均質(zhì)化處理，即把它們每一個(gè)都設(shè)置為零級(jí)，來仿真一個(gè)特征頻率問題。可在官網(wǎng)查看下方案例。

• 振弦
• 振膜
• 預(yù)應(yīng)力螺栓 Tonpilz 型壓電換能器
• 三維偏壓諧振器：穩(wěn)態(tài)，特征頻率，頻域和吸合分析
• 電感器中的小信號(hào)分析
• MOSFET 小信號(hào)分析
• 電化學(xué)阻抗譜

頻域激勵(lì)引起的非線性問題怎么解決？

到目前為止，我們所介紹的例子都假設(shè)系統(tǒng)對(duì)頻域載荷的響應(yīng)是線性的。也就是說，我們之前假設(shè)，如果任何一個(gè)頻域載荷或約束( )的大小增加了一個(gè)標(biāo)量值，那么頻域解的大小將增加相同的標(biāo)量值。當(dāng)然，要使這樣的假設(shè)成立，載荷、約束和材料屬性必須都與頻域解 無關(guān)。但是，在很多情況下這是不正確的。讓我們來看看如何解決其中的一些情況。

我們可以從材料屬性取決于循環(huán)平均解的情況開始。由于場(chǎng) 是復(fù)值，循環(huán)平均的大小由給出 。這使我們能夠求解以下形式的控制方程。

(4)

這種非線性偏微分方程實(shí)際上可以用我們的求解器系列文章中描述的完全相同的算法來求解。因此，除了輸入適當(dāng)?shù)牟牧戏蔷€性表達(dá)式之外，我們幾乎不需要學(xué)習(xí)任何 “額外 “的東西來解決這類問題。關(guān)于這種問題的例子，請(qǐng)看我們的 BK-7 光學(xué)玻璃中的自聚焦教程模型，其中折射率 ，直接取決于電磁場(chǎng)強(qiáng)度 I。

材料屬性不需要是周期平均幅度的這樣一個(gè)簡(jiǎn)單函數(shù)。例如，AC/DC 模塊包括一個(gè)有效的 H-B 曲線建模方法，該方法使用了之前這篇關(guān)于在頻域中為磁性材料建模的文章中描述的非線性材料關(guān)系。

到目前為止，我們只考慮了相對(duì)于周期平均場(chǎng)強(qiáng)而言的非線性材料響應(yīng)。然而，系統(tǒng)上的正弦激勵(lì)也有可能耦合成系統(tǒng)的更高階次的諧波激勵(lì)。為了理解為什么會(huì)這樣，請(qǐng)記住，我們的激勵(lì) 在時(shí)間上是變化的，而且我們已經(jīng)假設(shè)我們的解也將在時(shí)間上以相同的頻率 呈正弦波變化。但是，如果有任何材料的響應(yīng)直接取決于瞬時(shí)（而不是周期平均）的場(chǎng)強(qiáng)，那么我們可以使用三角關(guān)系 來推斷，該響應(yīng)實(shí)際上是這樣的： 。

這種類型的反應(yīng)，被稱為倍頻 或 高次諧波 的產(chǎn)生，在電磁學(xué)中，特別是光學(xué)系統(tǒng)中相當(dāng)普遍。盡管事實(shí)上可能有許多高次諧波，但實(shí)際上，只有一個(gè)或兩個(gè)高次諧波可能具有工程意義。對(duì)于這種情況，我們可以寫一些新的一般控制方程：

(5)

其中，在兩組方程之間有一個(gè)一般域的耦合項(xiàng) Q。為了簡(jiǎn)單起見，省略了靜態(tài)成分。同時(shí)請(qǐng)記住，所有的材料屬性都可以依賴于頻率，因此對(duì)于不同的諧波也會(huì)有所不同。現(xiàn)在，我們所具有的是一組帶有非線性耦合項(xiàng)的控制偏微分方程。求解這些方程只需要尋找我們?cè)谇蠼馄飨盗形恼轮薪榻B的同樣的求解方法。

下載這個(gè)教程模型，您將會(huì)看到一個(gè)演示頻域中的二次諧波產(chǎn)生的模型例子。

求解更多的廣義非線性問題

確實(shí)有一點(diǎn)被我們一帶而過了，就是不能再利用我們?cè)谶@里討論的假設(shè)來簡(jiǎn)化問題，即使有正弦波的激勵(lì)。在這種情況下，通常會(huì)想把重點(diǎn)轉(zhuǎn)移到時(shí)域建模上。盡管在時(shí)域建模會(huì)比在頻域建模花費(fèi)更多的時(shí)間，但可以捕獲到解的全部時(shí)間演變，并納入任何種類的非線性，甚至是導(dǎo)致非正弦響應(yīng)的非線性。

在 COMSOL 應(yīng)用庫(kù)中，你可以找到幾個(gè)時(shí)域建模的一般例子，包括：

• 非線性聲學(xué)-一維 Westervelt 方程建模
• 流體流動(dòng)中的梁振動(dòng)
• 高斯光束的二次諧波產(chǎn)生(RF)

如果你對(duì)這里討論的建模方法有任何疑問，并認(rèn)為它們對(duì)你的多物理場(chǎng)建模需求有用，請(qǐng)隨時(shí)聯(lián)系我們。